
Introduction
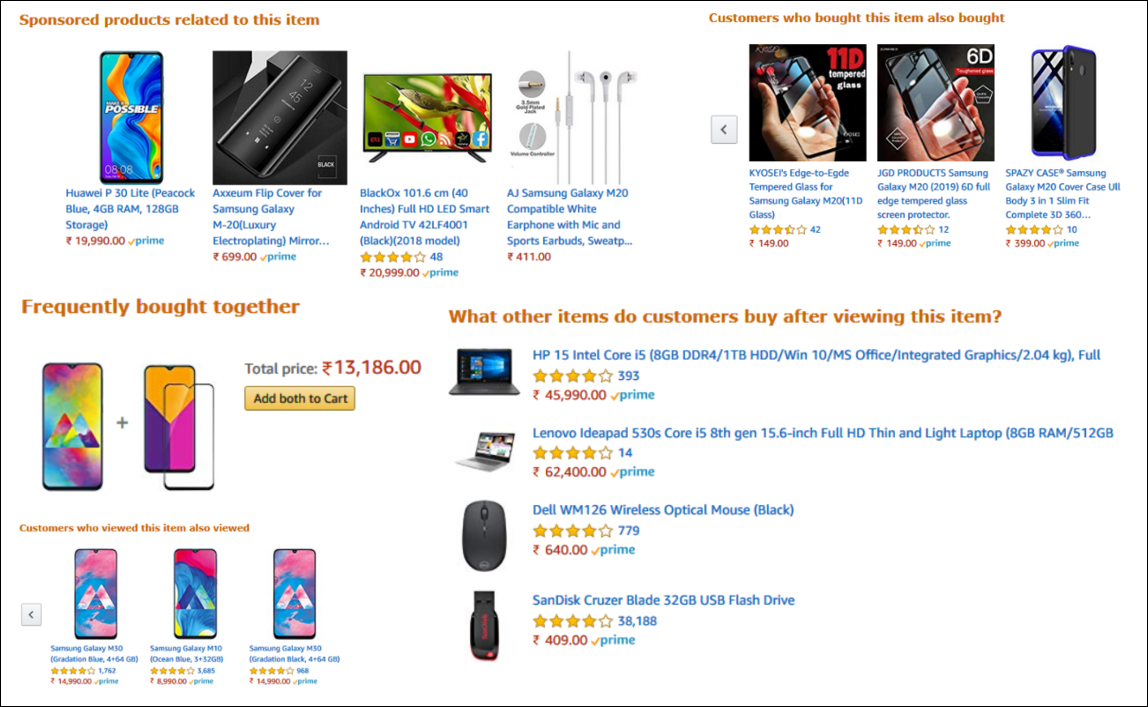
Ever wondered why items are displayed in a particular way in retail/online stores. Why certain items are suggested to you based on what you have added to the cart? Blame it on market basket analysis or association rule mining.
Resources
Below are the links to all the resources related to this post:
What?
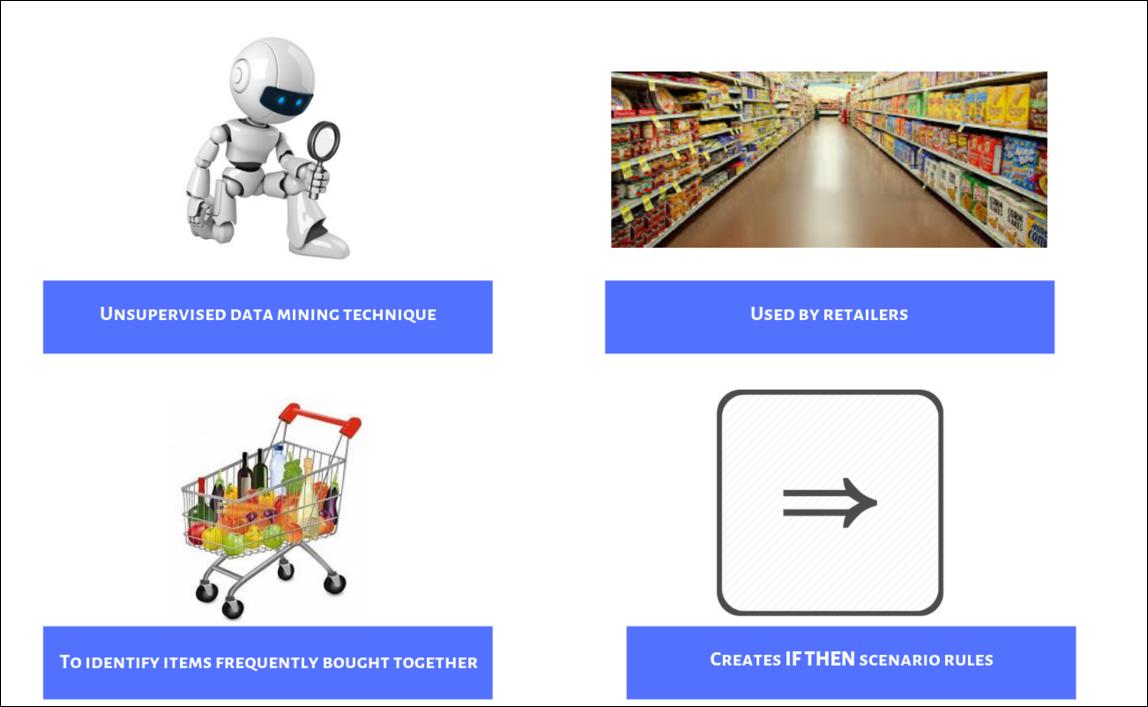
Market basket analysis uses association rule mining under the hood to identify products frequently bought together. Before we get into the nitty gritty of market basket analysis, let us get a basic understanding of association rule mining. It finds association between different objects in a set. In the case of market basket analysis, the objects are the products purchased by a cusomter and the set is the transaction. In short, market basket analysis
- is a unsupervised data mining technique
- that uncovers products frequently bought together
- and creates if-then scenario rules
Why ?
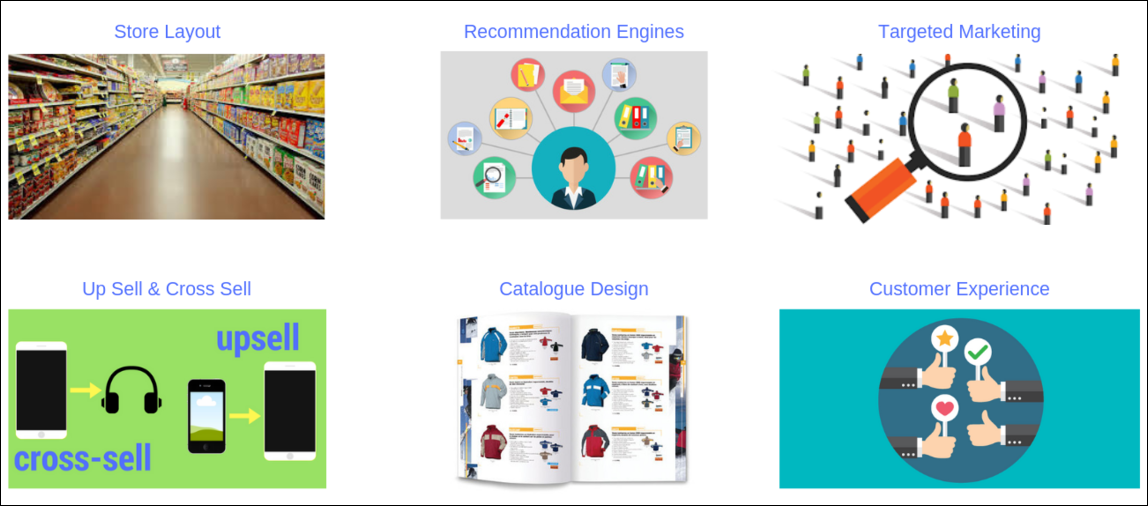
Market basket analysis creates actionable insights for:
- designing store layout
- online recommendation engines
- targeted marketing campaign/sales promotion/email campaign
- cross/up selling
- catalogue design
Advantages

Market basket analysisis is cost effective as data required is readily available through electronic point of sale systems. It generates actionable insights for product placement, cross/up selling strategies, targeted marketing campaigns, catalogue design, pricing strategies, inventory control etc.
Use Cases

Association rule mining has applications in several industries including retail, telecommunications, banking, insurance, manufacturing and medical. Let us look at its applications in more detail in the following industries:
Retail
The introduction of electronic point of sale systems have allowed the collection of immense amounts of data and retail organizations make prolifc use of market basket analysis for
- designing store layout so that consumers can more easily find items that are frequently purchased together
- recommending associated products that are frequently bought together, “Customers who purchased this product also viewed this product…”
- emailing customers who bought products specific products with other products and offers on those products that are likely to be interesting to them.
- grouping products that customers purchase frequently together in the store’s product placement
- designing special promotions that combine or discount certain products
- optimizing the layout of the catalog of an eCommerce site
- controlling inventory based on product demands and what products sell better together
Banks
Banks and financial institutions use market basket analysis to analyze credit card purchases for fraud detection and cross sell insurance products, investment products (mutual funds etc.), tax preparation, retirement planning, wealth management etc. It can also be used for next best offer, sequence and seasonal offers.
Telecommunications
The telecommunications industry is characterized by high volatility and low customer loyalty due to lucrative offers for new customers from other service providers. The more services a customer uses from a particular operator, the harder it gets for him/her to switch to another operator. Market basket analysis is used to bundle mobile, landline, TV and internet services to customers to increase stickiness and reduce churn.

Simple Example

Before we move on to the case study, let us use a simple example to understand the important terminologies that we will come across in the rest of the tutorial. In the example, the transactions include the following products:
- mobile phones
- ear phones
- USB cable
- power bank
- screen guard
- mobile case cover
- modem/router
- mouse
- external hard drive
Steps
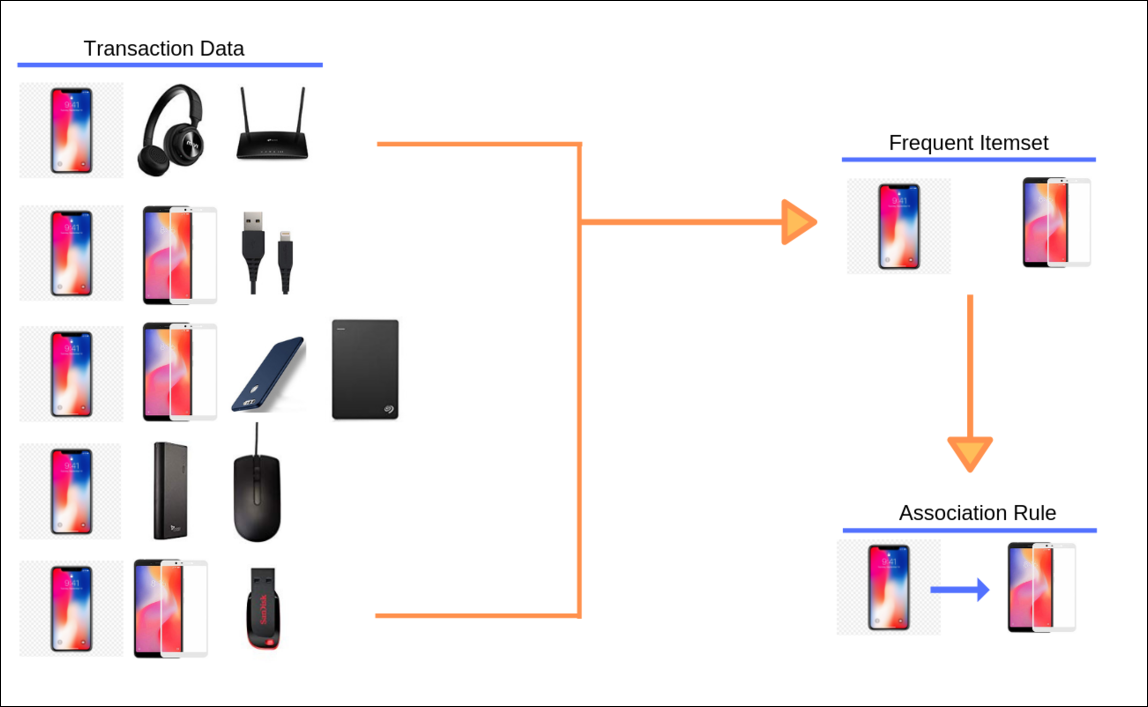
The two important steps in market basket analysis are:
- frequent itemset generation
- rules generation
We will discuss these steps in more detail in the case study.
Itemset
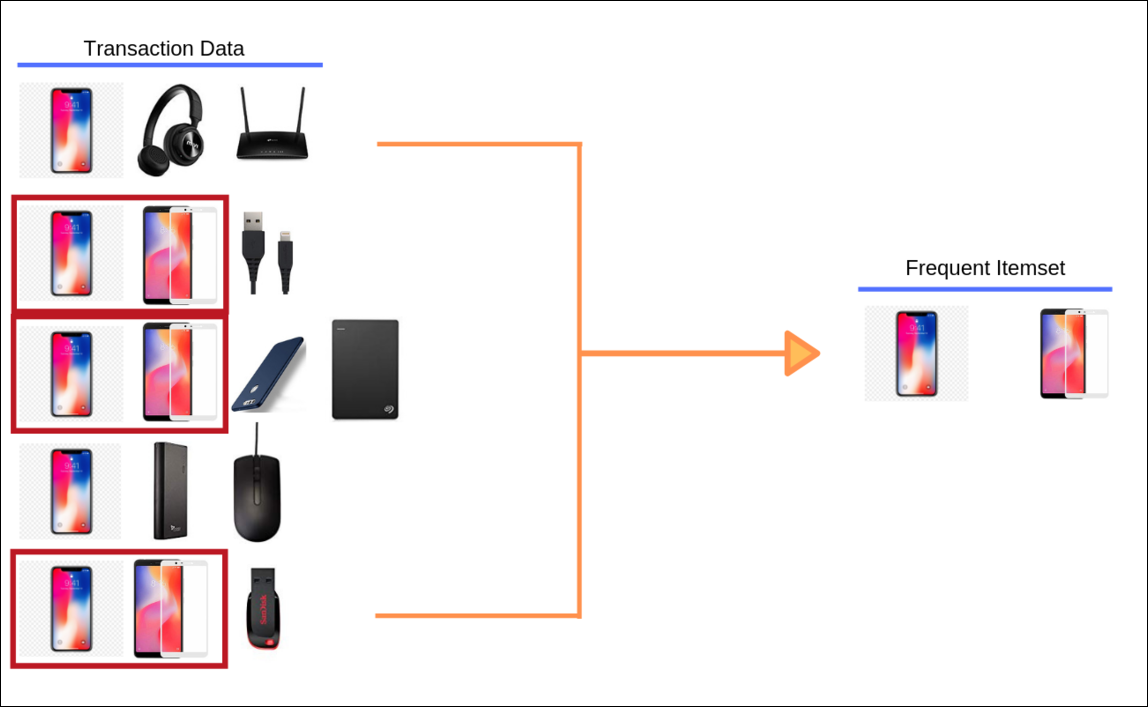
Itemset is the collection of items purchased by a customer. In our example, mobile phone and screen guard are a frequent intemset. They are present in 3 out of 5 transactions.
Antecedent & Consequent
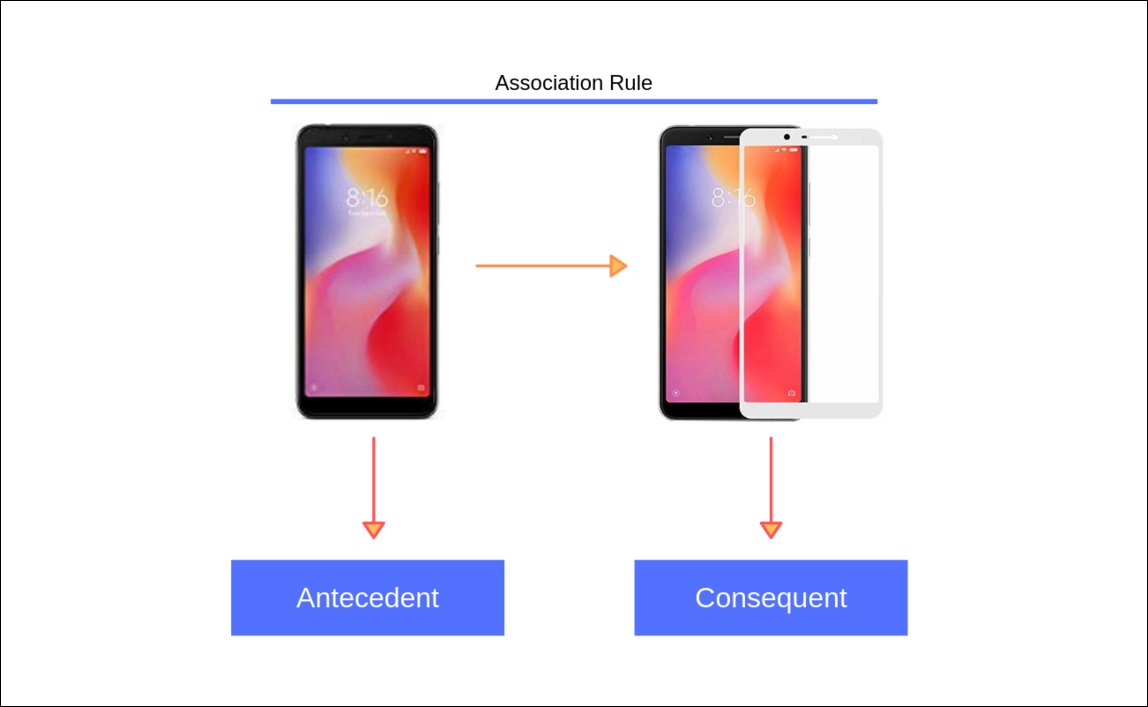
Antecedent is the items of the left hand side of the rule and consequent is the right hand side of the rule. In our example, mobile phone is the antecedent and screen guard is the consequent.
Support
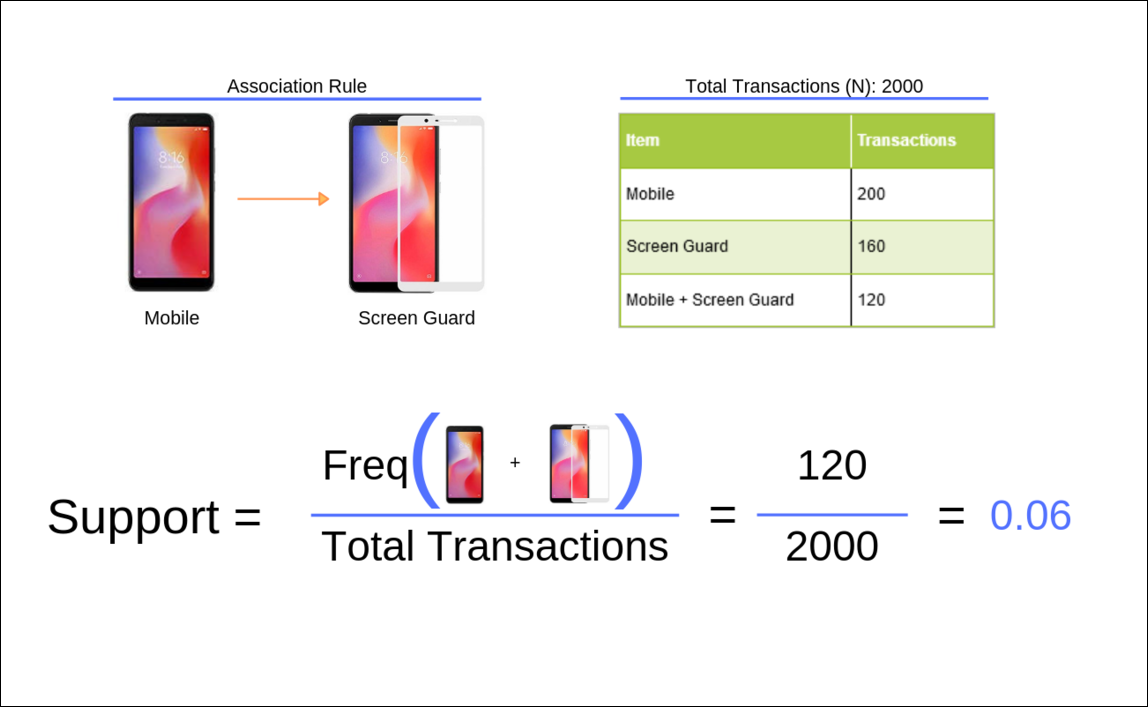
Support is the probability of the antecedent event occuring. It is the relative frequency of the itemset. If it is less than 50% then the association is considered less fruitful. In our example, support is the relative frequency of transactions that include both mobile phone and screen guard.
Confidence
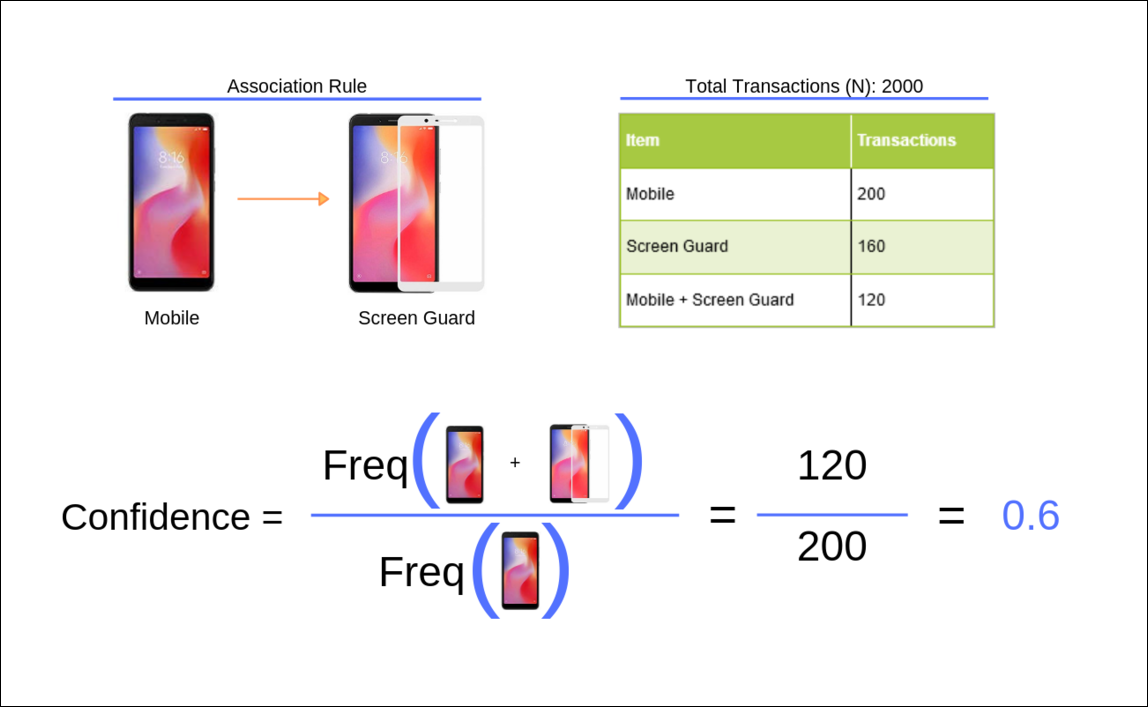
Confidence is the probability the consequent will co-occur with the antecedent. It expresses the operational efficiency of the rule. In our example, it is the probability that a customer will purchase screen guard provided that he has already bought the mobile phone.
Lift
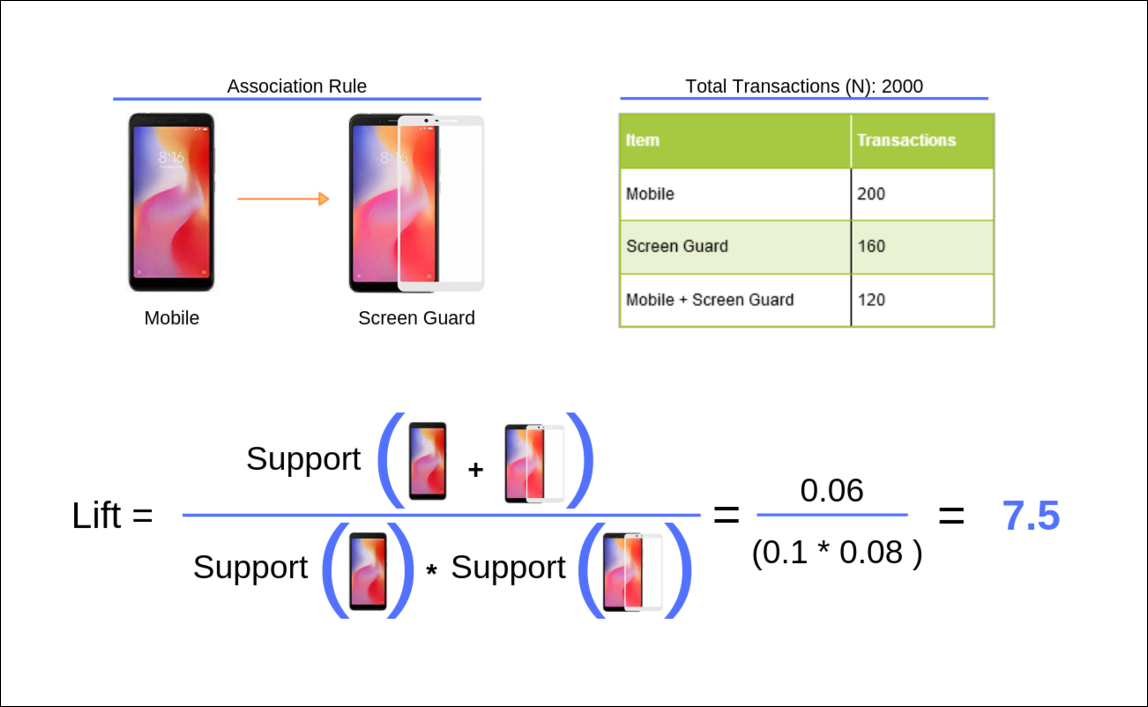
The lift ratio calculates the efficiency of the rule in finding consequences, compared to a random selection of transactions. Generally, a Lift ratio of greater than one suggests some applicability of the rule.To compute the lift for a rule, divide the support of the itemset by the product of the support for antecedent and consequent. Now, let us understand how to interpret lift.
Interpretation
- Lift = 1: implies no relationship between mobile phone and screen guard (i.e., mobile phone and screen guard occur together only by chance)
- Lift > 1: implies that there is a positive relationship between mobile phone and screen guard (i.e., mobile phone and screen guard occur together more often than random)
- Lift < 1: implies that there is a negative relationship between mobile phone and screen guard (i.e., mobile phone and screen guard occur together less often than random)
Data
Two public data sets are available for users to explore and learn market basket analysis:
The groceries data set is available in the arules package as well. In this tutorial, we will use the UCI data set as it closely resembles real world data sets giving us a chance to reshape the data and restructure it in format required by the arules package.
Data Dictionary
- invoice number
- stock code
- description
- quantity
- invoice date
- unit price
- customer id
- country
Libraries
library(readxl)
library(readr)
library(arules)
library(arulesViz)
library(magrittr)
library(dplyr)
library(lubridate)
library(forcats)
library(ggplot2)Preprocessing
This section is optional. You can skip to the Read Data section without any loss of continuity.
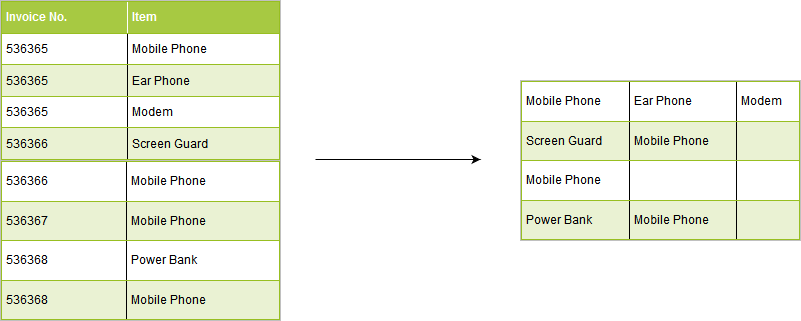
As shown above, the data set has one row per item. We have created a tiny R
package mbar,
for data pre-processing. It can be installed from GitHub as shown below:
# install.packages("devtools")
devtools::install_github("rsquaredacademy/mbar")We will use mbar_prep_data() from the mbar package to reshape the data so
that there is one row per transaction with items across columns excluding
the column names.
library(mbar)
mba_data <- read_excel("online-retail.xlsx")
transactions <- mbar_prep_data(mba_data, InvoiceNo, Description)
head(transactions)## # A tibble: 6 x 1,114
## item_1 item_2 item_3 item_4 item_5 item_6 item_7 item_8 item_9 item_10 item_11
## <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
## 1 WHITE~ "WHIT~ "CREA~ "KNIT~ "RED ~ "SET ~ "GLAS~ "" "" "" ""
## 2 HAND ~ "HAND~ "" "" "" "" "" "" "" "" ""
## 3 ASSOR~ "POPP~ "POPP~ "FELT~ "IVOR~ "BOX ~ "BOX ~ "BOX ~ "HOME~ "LOVE ~ "RECIP~
## 4 JAM M~ "RED ~ "YELL~ "BLUE~ "" "" "" "" "" "" ""
## 5 BATH ~ "" "" "" "" "" "" "" "" "" ""
## 6 ALARM~ "ALAR~ "ALAR~ "PAND~ "STAR~ "INFL~ "VINT~ "SET/~ "ROUN~ "SPACE~ "LUNCH~
## # ... with 1,103 more variables: item_12 <chr>, item_13 <chr>, item_14 <chr>,
## # item_15 <chr>, item_16 <chr>, item_17 <chr>, item_18 <chr>, item_19 <chr>,
## # item_20 <chr>, item_21 <chr>, item_22 <chr>, item_23 <chr>, item_24 <chr>,
## # item_25 <chr>, item_26 <chr>, item_27 <chr>, item_28 <chr>, item_29 <chr>,
## # item_30 <chr>, item_31 <chr>, item_32 <chr>, item_33 <chr>, item_34 <chr>,
## # item_35 <chr>, item_36 <chr>, item_37 <chr>, item_38 <chr>, item_39 <chr>,
## # item_40 <chr>, item_41 <chr>, item_42 <chr>, item_43 <chr>, item_44 <chr>,
## # item_45 <chr>, item_46 <chr>, item_47 <chr>, item_48 <chr>, item_49 <chr>,
## # item_50 <chr>, item_51 <chr>, item_52 <chr>, item_53 <chr>, item_54 <chr>,
## # item_55 <chr>, item_56 <chr>, item_57 <chr>, item_58 <chr>, item_59 <chr>,
## # item_60 <chr>, item_61 <chr>, item_62 <chr>, item_63 <chr>, item_64 <chr>,
## # item_65 <chr>, item_66 <chr>, item_67 <chr>, item_68 <chr>, item_69 <chr>,
## # item_70 <chr>, item_71 <chr>, item_72 <chr>, item_73 <chr>, item_74 <chr>,
## # item_75 <chr>, item_76 <chr>, item_77 <chr>, item_78 <chr>, item_79 <chr>,
## # item_80 <chr>, item_81 <chr>, item_82 <chr>, item_83 <chr>, item_84 <chr>,
## # item_85 <chr>, item_86 <chr>, item_87 <chr>, item_88 <chr>, item_89 <chr>,
## # item_90 <chr>, item_91 <chr>, item_92 <chr>, item_93 <chr>, item_94 <chr>,
## # item_95 <chr>, item_96 <chr>, item_97 <chr>, item_98 <chr>, item_99 <chr>,
## # item_100 <chr>, item_101 <chr>, item_102 <chr>, item_103 <chr>,
## # item_104 <chr>, item_105 <chr>, item_106 <chr>, item_107 <chr>,
## # item_108 <chr>, item_109 <chr>, item_110 <chr>, item_111 <chr>, ...EDA
Before we generate the rules using the arules package, let us explore the data set a bit.
What time of day do people purchase?
purchase_time <-
mba_data %>%
group_by(InvoiceDate) %>%
slice(1) %>%
mutate(time_of_day = hour(InvoiceDate)) %>%
pull(time_of_day) %>%
as.factor() %>%
fct_count()
purchase_time %>%
ggplot() +
geom_col(aes(x = f, y = n), fill = "blue") +
xlab("Hour of Day") + ylab("Transactions") +
ggtitle("Hourly Transaction Distribution") 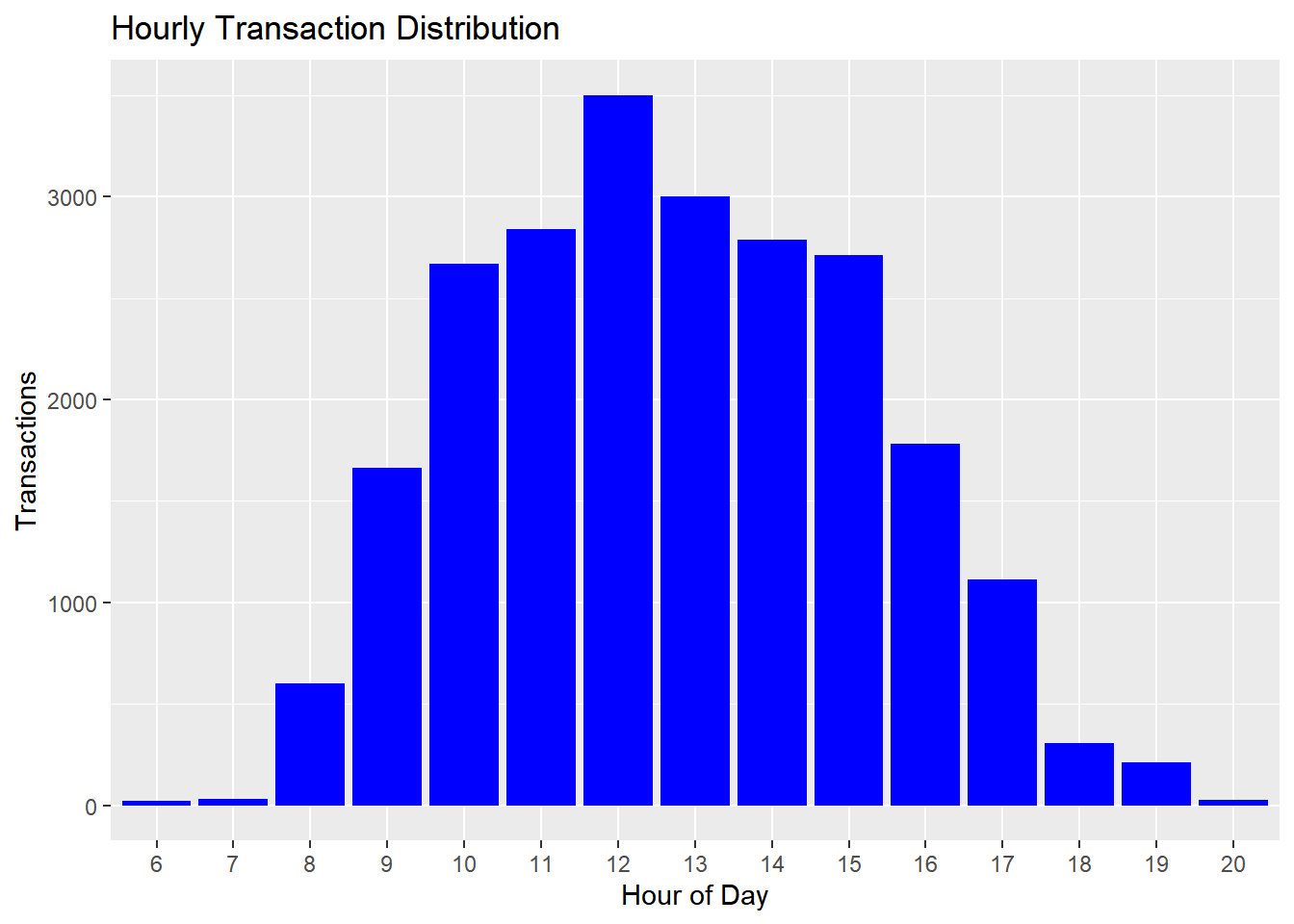
How many items are purchased on an average?
items <-
mba_data %>%
group_by(InvoiceNo) %>%
summarize(count = n()) %>%
pull(count) ## `summarise()` ungrouping (override with `.groups` argument)mean(items)## [1] 20.92313median(items)## [1] 10Most Purchased Items
mba_data %>%
group_by(Description) %>%
summarize(count = n()) %>%
arrange(desc(count))## `summarise()` ungrouping (override with `.groups` argument)## # A tibble: 4,212 x 2
## Description count
## <chr> <int>
## 1 WHITE HANGING HEART T-LIGHT HOLDER 2369
## 2 REGENCY CAKESTAND 3 TIER 2200
## 3 JUMBO BAG RED RETROSPOT 2159
## 4 PARTY BUNTING 1727
## 5 LUNCH BAG RED RETROSPOT 1638
## 6 ASSORTED COLOUR BIRD ORNAMENT 1501
## 7 SET OF 3 CAKE TINS PANTRY DESIGN 1473
## 8 <NA> 1454
## 9 PACK OF 72 RETROSPOT CAKE CASES 1385
## 10 LUNCH BAG BLACK SKULL. 1350
## # ... with 4,202 more rowsAverage Order Value
total_revenue <-
mba_data %>%
group_by(InvoiceNo) %>%
summarize(order_sum = sum(UnitPrice)) %>%
pull(order_sum) %>%
sum()## `summarise()` ungrouping (override with `.groups` argument)total_transactions <-
mba_data %>%
group_by(InvoiceNo) %>%
summarize(n()) %>%
nrow()## `summarise()` ungrouping (override with `.groups` argument)total_revenue / total_transactions## [1] 96.47892Read Data
It is now time to read data into R. We will use read.transactions()
from arules package. The data cannot be read using read.csv() or
read_csv() owing to the way it is structured. We will read the
transaction_data.csv file as it contains the data we had modified
in the previous step. We need to specify the following in order to
read the data set:
- name of the data set within quotes (single or double)
- the format of the data, if each line represnts a transaction, use
basket, and if each line represents an item in the transaction, usesingle - the separator used to separate the items in a transaction
In our data set, each line represents a transaction and the items in the
transaction are separated by a ,.
basket_data <- read.transactions("transaction_data.csv", format = "basket",
sep = ",")
basket_data## transactions in sparse format with
## 25901 transactions (rows) and
## 10085 items (columns)The read.transactions() function allows you to read data where each row
represents a item and not a transaction. In that case, the format argument
should be set to the value single and the cols argument should specify
the names or positions of the columns that represent the transaction id and
item id. We tried to read data in this way as well but failed to do so.
However, the code is available below for other users to try and let us know if
you find a way to get it to work or spot any mistakes we may have made.
get_data <- read.transactions("retail.csv",
format = "single",
sep = ",",
cols = c("InvoiceNo", "item"))We were able to read the data when we removed the sep argument from the above
code, but the result from the summary() function was way different than what
we see in the next section i.e. it showed higher number of transactions and
items.
Data Summary
To get a quick overview of the data, use summary(). It will return the
following:
- number of transactions
- number of items
- most frequent items
- distribution of items
- five number summary
summary(basket_data)## transactions as itemMatrix in sparse format with
## 25901 rows (elements/itemsets/transactions) and
## 10085 columns (items) and a density of 0.001660018
##
## most frequent items:
## WHITE HANGING HEART T-LIGHT HOLDER REGENCY CAKESTAND 3 TIER
## 1999 1914
## JUMBO BAG RED RETROSPOT PARTY BUNTING
## 1806 1488
## LUNCH BAG RED RETROSPOT (Other)
## 1404 425005
##
## element (itemset/transaction) length distribution:
## sizes
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## 1454 4578 1727 1208 942 891 781 715 696 683 612 642 547 530 543 555
## 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
## 537 479 459 491 428 405 328 311 280 248 261 235 221 233 224 175
## 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
## 174 145 149 139 122 119 100 117 98 94 102 93 72 73 74 71
## 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
## 69 68 59 70 49 49 54 57 42 32 42 39 34 40 22 27
## 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
## 30 24 34 28 25 21 23 26 14 17 24 11 18 14 13 10
## 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
## 16 18 15 10 9 16 13 16 13 7 8 12 12 8 7 7
## 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111
## 4 7 9 5 8 8 4 5 7 2 3 7 9 4 7 4
## 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127
## 2 7 1 1 4 7 6 2 3 5 4 4 2 5 6 2
## 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144
## 1 4 3 6 6 3 4 3 2 1 1 3 8 5 3 4
## 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
## 4 6 2 3 1 4 3 2 4 7 3 3 5 2 4 5
## 162 163 164 167 168 169 170 171 172 173 174 175 176 177 178 179
## 1 2 1 3 5 2 2 4 3 1 3 5 1 2 2 2
## 180 181 182 183 184 185 186 187 189 190 192 193 194 196 197 198
## 2 1 2 1 2 1 1 2 2 1 1 5 1 2 3 2
## 201 202 204 205 206 207 208 209 212 213 215 219 220 224 226 227
## 1 1 2 2 1 3 3 2 1 2 2 7 1 3 3 1
## 228 230 232 234 236 238 240 241 244 248 249 250 252 256 257 258
## 1 2 1 2 1 2 2 2 1 1 2 2 1 1 1 1
## 260 261 263 265 266 270 272 281 284 285 298 299 301 303 304 305
## 2 1 2 1 1 1 1 1 1 2 1 2 1 1 1 3
## 312 314 316 320 321 326 327 329 332 333 338 339 341 344 348 350
## 2 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1
## 360 365 367 375 391 394 398 400 402 405 411 419 422 429 431 442
## 2 1 1 3 1 1 1 1 1 1 1 2 1 1 2 1
## 447 460 468 471 477 509 514 530 587 627 1114
## 1 1 1 1 1 1 1 1 1 1 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 2.00 8.00 16.74 20.00 1114.00
##
## includes extended item information - examples:
## labels
## 1 *Boombox Ipod Classic
## 2 *USB Office Mirror Ball
## 3 ?Item Frequency Plot
The most frequent items in the data set can be plotted using
itemFrequencyPlot(). We can specify the number of items to be plotted and
whether the Y axis should represent the absolute or relative number of transactions
that include the item.
The topN argument can be used to specify the number of items to be plotted
and the type argument can be used to specify whether the Y axis represents
absolute/relative frequency of the items.
itemFrequencyPlot(basket_data, topN = 10, type = 'absolute')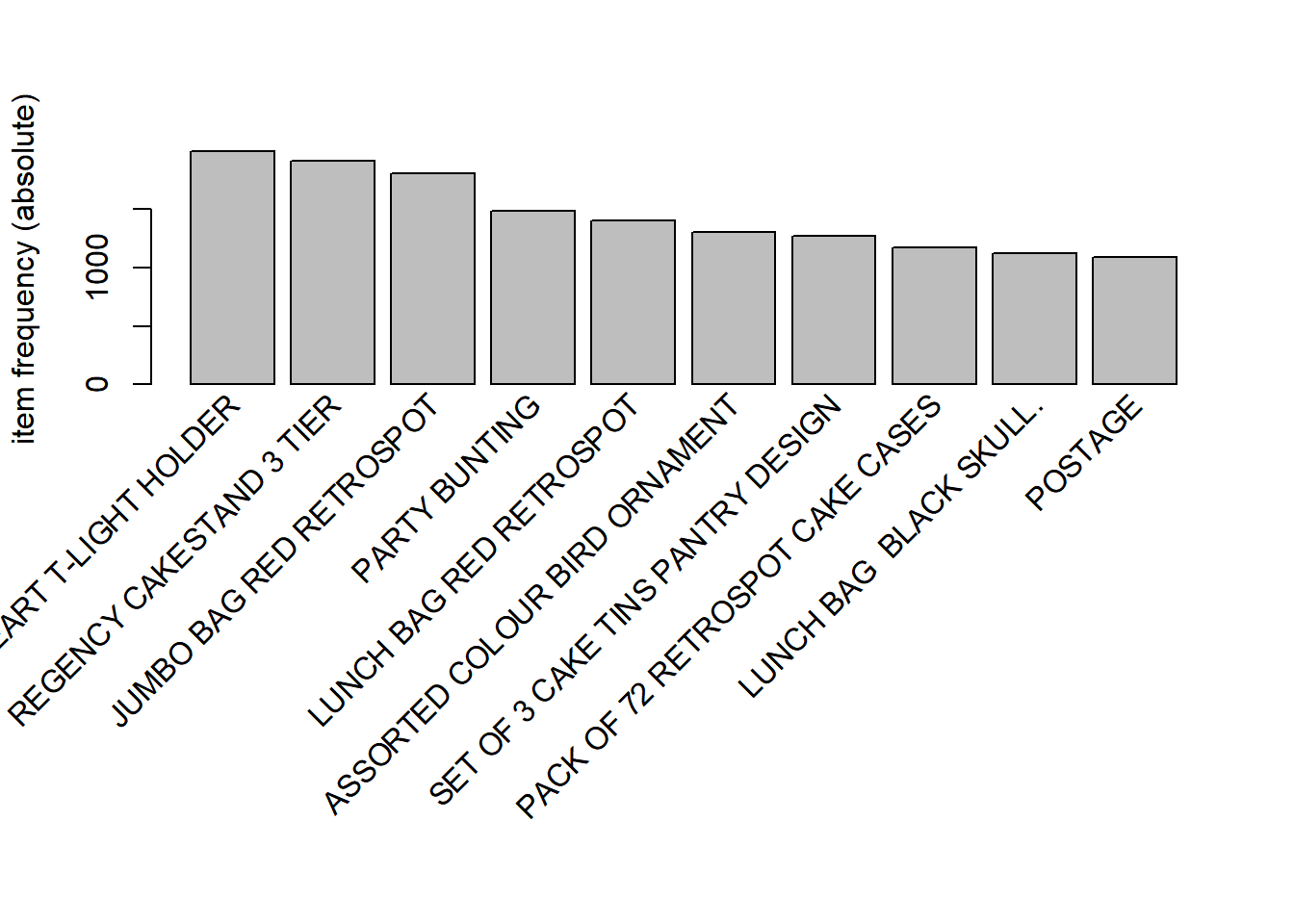
In the below plot, the Y axis represents the relative frequency of the items
plotted.
itemFrequencyPlot(basket_data, topN = 10, type = 'relative')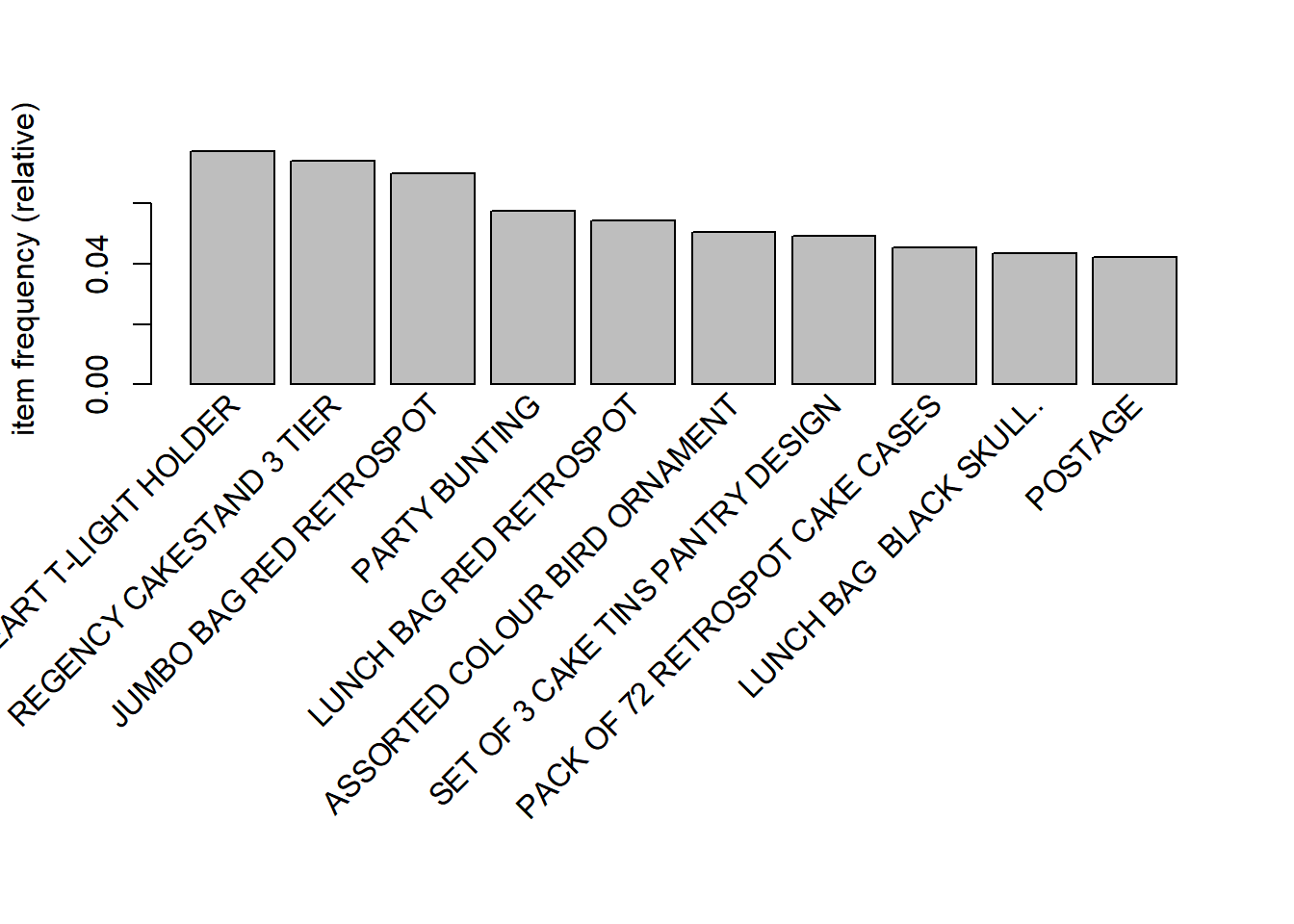

Generate Rules
Finally, to the part you all have been waiting for, rules generation. The
apriori() function is used for generating the rules. We will first learn the
different inputs that must be specified and later on play around with them and
see how the rules generated change.
The first input is the data set, which in our case is basket_data. Next, we
will supply the mining parameters using the parameter argument:
supp: minimum support for an itemsetconf: minimum confidencemaxlen: maximum number of items the antecedent may includetarget: the type of association mined i.e. rules
The parameter argument takes several additional inputs but to get started, it
is sufficient to know those mentioned above. All the inputs are supplied using
a list().
For our case study, we will specify the following:
- support: 0.009
- confidence: 0.8
- maxlen: 4
Keep in mind, mining association rules with very low values for support will
result in a large number of rules being generated, resulting in long execution
time and the process will eventually run out of memory.
rules <- apriori(basket_data, parameter = list(supp=0.009, conf=0.8,
target = "rules", maxlen = 4))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.009 1
## maxlen target ext
## 4 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 233
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[10085 item(s), 25901 transaction(s)] done [1.08s].
## sorting and recoding items ... [508 item(s)] done [0.02s].
## creating transaction tree ... done [0.06s].
## checking subsets of size 1 2 3 4## Warning in apriori(basket_data, parameter = list(supp = 0.009, conf = 0.8, :
## Mining stopped (maxlen reached). Only patterns up to a length of 4 returned!## done [0.07s].
## writing ... [22 rule(s)] done [0.00s].
## creating S4 object ... done [0.02s].Change the values of supp, conf and maxlen, and observe how the rules
generated change.
Rules Summary
Once the rules have been generated by apriori(), we can use summary() to
get some basic information such as rule length distribution.
summary(rules)## set of 22 rules
##
## rule length distribution (lhs + rhs):sizes
## 2 3 4
## 11 9 2
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 2.000 2.500 2.591 3.000 4.000
##
## summary of quality measures:
## support confidence coverage lift
## Min. :0.009034 Min. :0.8035 Min. :0.009614 Min. :22.59
## 1st Qu.:0.010453 1st Qu.:0.8530 1st Qu.:0.011592 1st Qu.:25.02
## Median :0.013223 Median :0.8868 Median :0.014362 Median :55.94
## Mean :0.012760 Mean :0.9120 Mean :0.014061 Mean :48.55
## 3rd Qu.:0.014362 3rd Qu.:1.0000 3rd Qu.:0.014362 3rd Qu.:61.23
## Max. :0.018339 Max. :1.0000 Max. :0.021544 Max. :71.30
## count
## Min. :234.0
## 1st Qu.:270.8
## Median :342.5
## Mean :330.5
## 3rd Qu.:372.0
## Max. :475.0
##
## mining info:
## data ntransactions support confidence
## basket_data 25901 0.009 0.8The output from summary() does not display the rules though. To view the
rules, we have to use inspect().
Inspect Rules
The inspect() function will display the rules along with:
- support
- confidence
- lift
- count
Before you inspect the rules, you can sort it by support, confidence or lift. In the below, output, we sort the rules by confidence in descending order before inspecting them.
basket_rules <- sort(rules, by = 'confidence', decreasing = TRUE)
inspect(basket_rules[1:10])## lhs rhs support confidence coverage lift count
## [1] {BACK DOOR} => {KEY FOB} 0.009613528 1.0000000 0.009613528 61.23168 249
## [2] {SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380 1.0000000 0.014362380 69.62634 372
## [3] {SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380 1.0000000 0.014362380 69.62634 372
## [4] {SET 3 RETROSPOT TEA} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [5] {SUGAR} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [6] {SHED} => {KEY FOB} 0.011273696 1.0000000 0.011273696 61.23168 292
## [7] {SET 3 RETROSPOT TEA,
## SUGAR} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [8] {COFFEE,
## SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380 1.0000000 0.014362380 69.62634 372
## [9] {COFFEE,
## SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380 1.0000000 0.014362380 69.62634 372
## [10] {PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER,
## ROSES REGENCY TEACUP AND SAUCER} => {GREEN REGENCY TEACUP AND SAUCER} 0.009999614 0.8900344 0.011235087 25.16679 259Redundant & Non Redundant Rules
Redundant Rules
A rule is redundant if a more general rules with the same or a higher confidence exists. That is, a more specific rule is redundant if it is only equally or even less predictive than a more general rule. A rule is more general if it has the same RHS but one or more items removed from the LHS.
Example 1
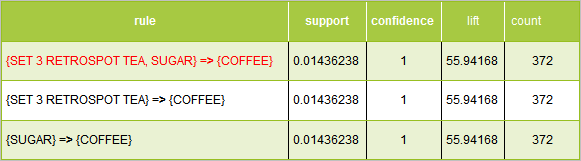
In the above example, the first rule has the same support, condifence and lift as the next two rules. The second item in the left hand side of the rule is not adding any value and as such makes the rule redundant.
Example 2
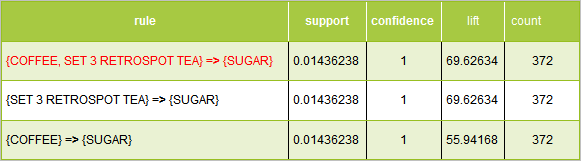
In the above example, the first two rules have the same support, condifence and lift. The third rule differs only with respect to lift.
Example 3
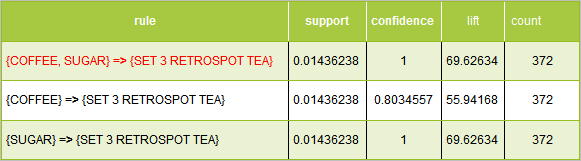
In the above example, the first and third rule have the same support, condifence and lift. The second rule is different with respect to confidence and lift.
Now that we have understood what redundant rules are and how to identify them, let us use the below R code to inspect them.
inspect(rules[is.redundant(rules)])## lhs rhs support confidence
## [1] {SET 3 RETROSPOT TEA,SUGAR} => {COFFEE} 0.01436238 1
## [2] {COFFEE,SET 3 RETROSPOT TEA} => {SUGAR} 0.01436238 1
## [3] {COFFEE,SUGAR} => {SET 3 RETROSPOT TEA} 0.01436238 1
## coverage lift count
## [1] 0.01436238 55.94168 372
## [2] 0.01436238 69.62634 372
## [3] 0.01436238 69.62634 372Non-redundant Rules
Now let us look at the non-redundant rules.
inspect(rules[!is.redundant(rules)])## lhs rhs support confidence coverage lift count
## [1] {REGENCY TEA PLATE PINK} => {REGENCY TEA PLATE GREEN} 0.009034400 0.8863636 0.010192657 71.29722 234
## [2] {BACK DOOR} => {KEY FOB} 0.009613528 1.0000000 0.009613528 61.23168 249
## [3] {SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380 1.0000000 0.014362380 69.62634 372
## [4] {SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380 1.0000000 0.014362380 69.62634 372
## [5] {SET 3 RETROSPOT TEA} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [6] {COFFEE} => {SET 3 RETROSPOT TEA} 0.014362380 0.8034557 0.017875758 55.94168 372
## [7] {SUGAR} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [8] {COFFEE} => {SUGAR} 0.014362380 0.8034557 0.017875758 55.94168 372
## [9] {REGENCY TEA PLATE GREEN} => {REGENCY TEA PLATE ROSES} 0.010347091 0.8322981 0.012431952 55.99313 268
## [10] {SHED} => {KEY FOB} 0.011273696 1.0000000 0.011273696 61.23168 292
## [11] {SET/6 RED SPOTTY PAPER CUPS} => {SET/6 RED SPOTTY PAPER PLATES} 0.012084476 0.8087855 0.014941508 44.38211 313
## [12] {SET/20 RED RETROSPOT PAPER NAPKINS,
## SET/6 RED SPOTTY PAPER CUPS} => {SET/6 RED SPOTTY PAPER PLATES} 0.009111617 0.8872180 0.010269874 48.68609 236
## [13] {PINK REGENCY TEACUP AND SAUCER,
## ROSES REGENCY TEACUP AND SAUCER} => {GREEN REGENCY TEACUP AND SAUCER} 0.018339060 0.8828996 0.020771399 24.96505 475
## [14] {GREEN REGENCY TEACUP AND SAUCER,
## PINK REGENCY TEACUP AND SAUCER} => {ROSES REGENCY TEACUP AND SAUCER} 0.018339060 0.8512545 0.021543570 22.59051 475
## [15] {PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER} => {ROSES REGENCY TEACUP AND SAUCER} 0.011235087 0.8584071 0.013088298 22.78033 291
## [16] {PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER} => {GREEN REGENCY TEACUP AND SAUCER} 0.011312305 0.8643068 0.013088298 24.43931 293
## [17] {STRAWBERRY CHARLOTTE BAG,
## WOODLAND CHARLOTTE BAG} => {RED RETROSPOT CHARLOTTE BAG} 0.010771785 0.8110465 0.013281340 23.65644 279
## [18] {PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER,
## ROSES REGENCY TEACUP AND SAUCER} => {GREEN REGENCY TEACUP AND SAUCER} 0.009999614 0.8900344 0.011235087 25.16679 259
## [19] {GREEN REGENCY TEACUP AND SAUCER,
## PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER} => {ROSES REGENCY TEACUP AND SAUCER} 0.009999614 0.8839590 0.011312305 23.45843 259What influenced purchase of product X?
So far, we have learnt how to generate, inspect and prune rules. Now, how do we use these rules? To make business sense, we need to come up with a set of rules that can be used either for product placement in physical stores or as recommendations in an online store or for targeted marketing via email campaigns etc. To achieve that, we need to know 2 things:
- what products influenced the purchase of product X?
- what purchases did product X influence?
For our case study, we can modify the above questions as:
What influenced the purchase of sugar?
To view the products which influenced the purchase of sugar, we will
continue to use the apriori() function but add one more argument, appearance.
It restricts the appearance of the items. Since we want the right hand side of
the rules to have only one value, sugar, we will set the rhs argument to
sugar. The left hand side of the rules should include all the products that
influenced the purchase of sugar i.e. it will exclude sugar. We will use
the default argument and supply it the value lhs i.e. all items excluding
sugar can appear on the left hand side of the rule by default.
defaultrhs
sugar_rules <- apriori(basket_data, parameter = list(supp = 0.009, conf = 0.8),
appearance = list(default = "lhs", rhs = "SUGAR")) ## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.009 1
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 233
##
## set item appearances ...[1 item(s)] done [0.00s].
## set transactions ...[10085 item(s), 25901 transaction(s)] done [0.86s].
## sorting and recoding items ... [508 item(s)] done [0.02s].
## creating transaction tree ... done [0.04s].
## checking subsets of size 1 2 3 4 done [0.07s].
## writing ... [3 rule(s)] done [0.00s].
## creating S4 object ... done [0.02s].rules_sugar <- sort(sugar_rules, by = "confidence", decreasing = TRUE)
inspect(rules_sugar)## lhs rhs support confidence coverage
## [1] {SET 3 RETROSPOT TEA} => {SUGAR} 0.01436238 1.0000000 0.01436238
## [2] {COFFEE,SET 3 RETROSPOT TEA} => {SUGAR} 0.01436238 1.0000000 0.01436238
## [3] {COFFEE} => {SUGAR} 0.01436238 0.8034557 0.01787576
## lift count
## [1] 69.62634 372
## [2] 69.62634 372
## [3] 55.94168 372For the support and confidence we have mentioned, we know the following products influenced the purchase of sugar:
- COFFEE
- SET 3 RETROSPOT TEA
What purchases did product X influence?
Now that we know what products influenced the purchase of sugar, let us answer the second question.
What purchases did sugar influence?
In this case, we want sugar to be on the left hand side of the rule and all
the products it influenced to be on the right hand side. We set the lhs
argument to sugar and the default argument to rhs as all the products,
the purchase of which was influenced by sugar should appear on the left
hand side of the rule by default.
sugar_rules <- apriori(basket_data, parameter = list(supp = 0.009, conf = 0.8),
appearance = list(default = "rhs", lhs = "SUGAR")) ## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.009 1
## maxlen target ext
## 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 233
##
## set item appearances ...[1 item(s)] done [0.00s].
## set transactions ...[10085 item(s), 25901 transaction(s)] done [0.76s].
## sorting and recoding items ... [508 item(s)] done [0.02s].
## creating transaction tree ... done [0.03s].
## checking subsets of size 1 2 done [0.01s].
## writing ... [2 rule(s)] done [0.00s].
## creating S4 object ... done [0.01s].rules_sugar <- sort(sugar_rules, by = "confidence", decreasing = TRUE)
inspect(rules_sugar)## lhs rhs support confidence coverage lift
## [1] {SUGAR} => {SET 3 RETROSPOT TEA} 0.01436238 1 0.01436238 69.62634
## [2] {SUGAR} => {COFFEE} 0.01436238 1 0.01436238 55.94168
## count
## [1] 372
## [2] 372For the support and confidence we have mentioned, we know the purchase of the following products were influenced by sugar:
- COFFEE
- SET 3 RETROSPOT TEA
Top Rules
Let us take a look at the top rules by
Support
supp_rules <- sort(rules, by = 'support', decreasing = TRUE)
top_rules <- supp_rules[1:10]
inspect(top_rules)## lhs rhs support confidence coverage lift count
## [1] {PINK REGENCY TEACUP AND SAUCER,
## ROSES REGENCY TEACUP AND SAUCER} => {GREEN REGENCY TEACUP AND SAUCER} 0.01833906 0.8828996 0.02077140 24.96505 475
## [2] {GREEN REGENCY TEACUP AND SAUCER,
## PINK REGENCY TEACUP AND SAUCER} => {ROSES REGENCY TEACUP AND SAUCER} 0.01833906 0.8512545 0.02154357 22.59051 475
## [3] {SET 3 RETROSPOT TEA} => {SUGAR} 0.01436238 1.0000000 0.01436238 69.62634 372
## [4] {SUGAR} => {SET 3 RETROSPOT TEA} 0.01436238 1.0000000 0.01436238 69.62634 372
## [5] {SET 3 RETROSPOT TEA} => {COFFEE} 0.01436238 1.0000000 0.01436238 55.94168 372
## [6] {COFFEE} => {SET 3 RETROSPOT TEA} 0.01436238 0.8034557 0.01787576 55.94168 372
## [7] {SUGAR} => {COFFEE} 0.01436238 1.0000000 0.01436238 55.94168 372
## [8] {COFFEE} => {SUGAR} 0.01436238 0.8034557 0.01787576 55.94168 372
## [9] {SET 3 RETROSPOT TEA,
## SUGAR} => {COFFEE} 0.01436238 1.0000000 0.01436238 55.94168 372
## [10] {COFFEE,
## SET 3 RETROSPOT TEA} => {SUGAR} 0.01436238 1.0000000 0.01436238 69.62634 372Confidence
conf_rules <- sort(rules, by = 'confidence', decreasing = TRUE)
top_rules <- conf_rules[1:10]
inspect(top_rules)## lhs rhs support confidence coverage lift count
## [1] {BACK DOOR} => {KEY FOB} 0.009613528 1.0000000 0.009613528 61.23168 249
## [2] {SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380 1.0000000 0.014362380 69.62634 372
## [3] {SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380 1.0000000 0.014362380 69.62634 372
## [4] {SET 3 RETROSPOT TEA} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [5] {SUGAR} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [6] {SHED} => {KEY FOB} 0.011273696 1.0000000 0.011273696 61.23168 292
## [7] {SET 3 RETROSPOT TEA,
## SUGAR} => {COFFEE} 0.014362380 1.0000000 0.014362380 55.94168 372
## [8] {COFFEE,
## SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380 1.0000000 0.014362380 69.62634 372
## [9] {COFFEE,
## SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380 1.0000000 0.014362380 69.62634 372
## [10] {PINK REGENCY TEACUP AND SAUCER,
## REGENCY CAKESTAND 3 TIER,
## ROSES REGENCY TEACUP AND SAUCER} => {GREEN REGENCY TEACUP AND SAUCER} 0.009999614 0.8900344 0.011235087 25.16679 259Lift
lift_rules <- sort(rules, by = 'lift', decreasing = TRUE)
top_rules <- lift_rules[1:10]
inspect(top_rules)## lhs rhs support
## [1] {REGENCY TEA PLATE PINK} => {REGENCY TEA PLATE GREEN} 0.009034400
## [2] {SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380
## [3] {SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380
## [4] {COFFEE,SET 3 RETROSPOT TEA} => {SUGAR} 0.014362380
## [5] {COFFEE,SUGAR} => {SET 3 RETROSPOT TEA} 0.014362380
## [6] {BACK DOOR} => {KEY FOB} 0.009613528
## [7] {SHED} => {KEY FOB} 0.011273696
## [8] {REGENCY TEA PLATE GREEN} => {REGENCY TEA PLATE ROSES} 0.010347091
## [9] {SET 3 RETROSPOT TEA} => {COFFEE} 0.014362380
## [10] {COFFEE} => {SET 3 RETROSPOT TEA} 0.014362380
## confidence coverage lift count
## [1] 0.8863636 0.010192657 71.29722 234
## [2] 1.0000000 0.014362380 69.62634 372
## [3] 1.0000000 0.014362380 69.62634 372
## [4] 1.0000000 0.014362380 69.62634 372
## [5] 1.0000000 0.014362380 69.62634 372
## [6] 1.0000000 0.009613528 61.23168 249
## [7] 1.0000000 0.011273696 61.23168 292
## [8] 0.8322981 0.012431952 55.99313 268
## [9] 1.0000000 0.014362380 55.94168 372
## [10] 0.8034557 0.017875758 55.94168 372
Visualization
To visualize the rules, the authors of arules have created a companion
package, arulesViz. It offers several options for visualizing the rules
generated by apriori().
Scatter Plot
We can use the default plot() method to create a scatter plot. It will plot
the support on the X axis, the confidence on the Y axis and the lift is
represented by the opaqueness/alpha of the color of the points.
plot(basket_rules)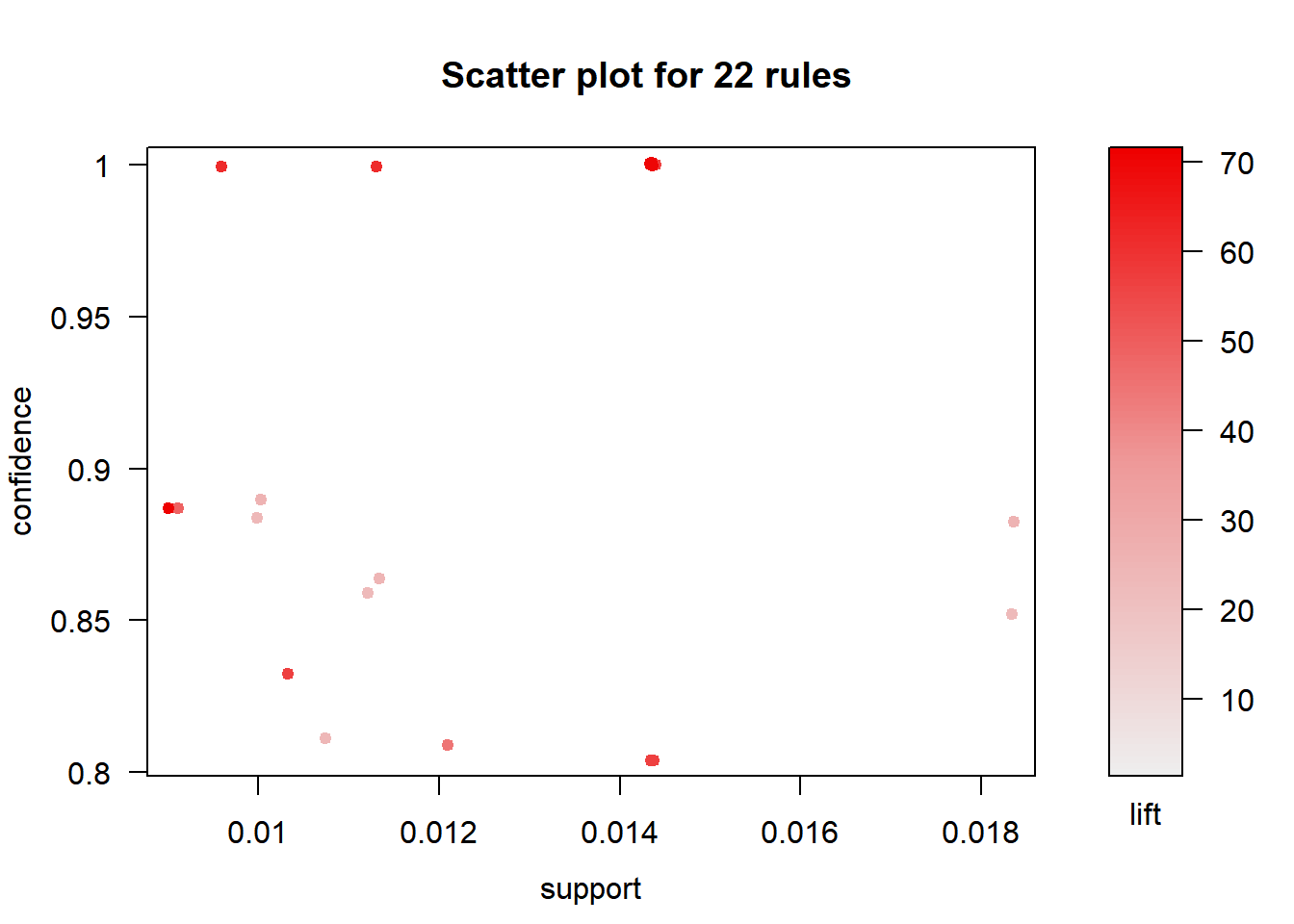
Network Plot
We can create a network plot using the method argument and supplying it the
value graph. You can see the directionality of the rule in the below plot.
For example, people who buy shed also buy key fob and similarly, people
who buy back door also buy key fob. It will be difficult to identify
the directionality of the rules when we are trying to plot too many rules.
The method argument takes several other values as well.
plot(top_rules, method = 'graph')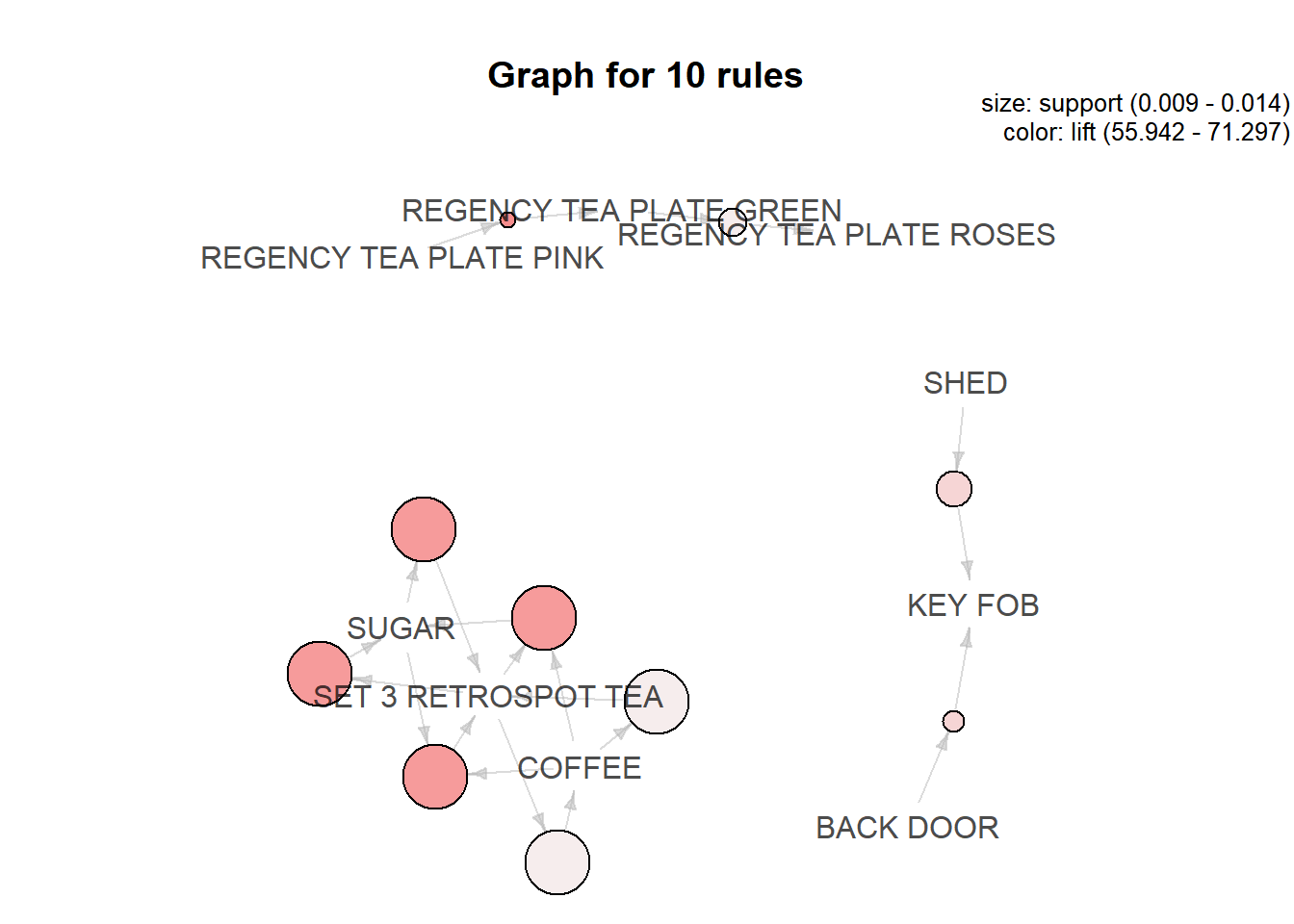
Things to keep in mind..
Directionality of rule is lost while using lift
The directionality of a rule is lost while using lift. In the below example, the lift is same for both the following rules:
- {Mobile Phone} => {Screen Guard}
- {Screen Guard} => {Mobile Phone}
It is clear that the lift is the same irrespective of the direction of the rule.

Confidence as a measure can be misleading
If you look at the below example, the confidence for the second rule, {Screen Guard} => {Mobile Phone}, is greater than the first rule, {Mobile Phone} => {Screen Guard}. It does not mean that we can recommend a mobile phone to a customer who is purchasing a screen guard. It is important to ensure that we do not use rules just because they have high confidence associated with them.

Summary
- market basket analysis is an unsupervised data mining technique
- uncovers products frequently bought together
- creates if-then scenario rules
- cost-effective, insightful and actionable
- association rule mining has applications in several industries
- directionality of rule is lost while using lift
- confidence as a measure can be misleading
Your knowledge of the domain/business matters a lot when you are trying to use market basket analysis. Especially, when you are trying to select or shortlist rules and use them for product placement in a store or for recommending products online. It is a good practice to critically review the rules before implementing them.
